红黑树
发明红黑树的人是天才!
1 2-3-4 树特性
2-3-4 树是一个由下向上生成的多叉树,又名 4 阶 B 树(Balance Tree),是一种多路查找树。红黑树是一个特殊的 2-3-4 树。
2-3-4 树节点:
- 2-节点:包含 1 个元素的节点,有 2 个子节点
- 3-节点:包含 2 个元素的节点,有 3 个子节点
- 4-节点:包含 3 个元素的节点,有 4 个子节点
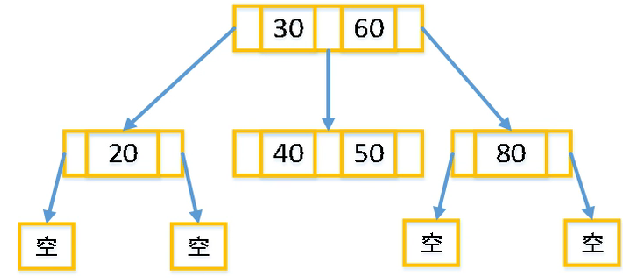
2-3-4 树可以大大压缩树的高度,提升查找性能。
2-3-4 树的特性:
- 元素整体上保持二叉树搜索的性质,即父节点大于左子节点,小于右子节点
- 节点包含多个元素时,元素的排列顺序必须是从左到右从小到大
- 所有的叶子节点都在最底层,所有的非叶子节点必须连满
- 2-3-4 树的形成过程 [可视化工具](B-Tree Visualization (usfca.edu))
2 红黑树的特性
- 节点分为红色和黑色
- 树的根节点是黑色
- 红色节点不可以相邻
- 黑色节点可以相邻,在红黑树中,叶子节点指的是 null 节点,且认为 null 叶子节点是黑色
- 从任何一个节点到其任何后代 null 叶子节点的路径都具有相同数量的黑色节点
3 2-3-4 树和红黑树关系
- 2-3-4 树的查询操作像普通的二叉搜索树一样,但由于其节点元素数不确定,实现起来并不方便,一般使用它的等同变形——红黑树
- 2-3-4 树的每一个结点都对应红黑树的一种结构,所以每一棵 2-3-4 树也都对应一棵红黑树
3.1 红黑树和 2-3-4 树的等价关系
红黑树起源于 2-3-4 树,本质上就是一颗 2-3-4 树。
- 一个 2 节点对应的 2-3-4 树节点就是一个红黑树黑色节点
- 一个 3 节点可以对应两种情况的红黑树节点,一种是左倾,一种是右倾,所以一个 2-3-4 树可以有多个对应的红黑树
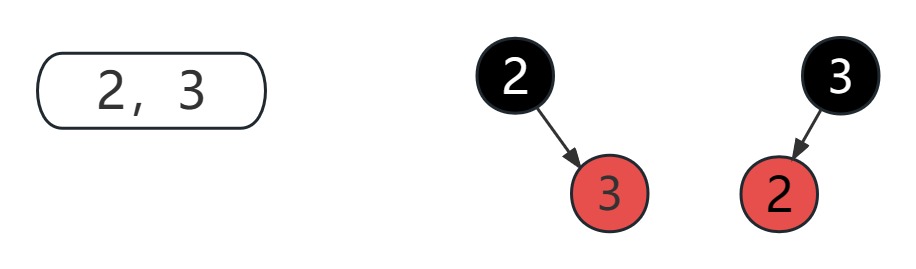
- 一个 4 节点对应的红黑树情况只有一种,中间节点黑色,左右节点红色
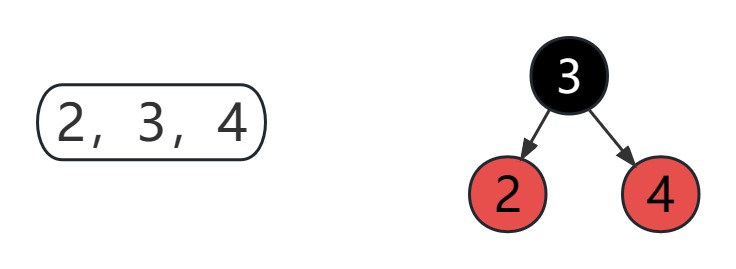
- 裂变状态
- 当给 4-节点再添加新节点时,新节点为红色,由于不能有两个连续的红色节点,需要将原来节点颜色互换
- 新升元的红 3 节点作为新节点再向上回溯调整平衡,直至根节点
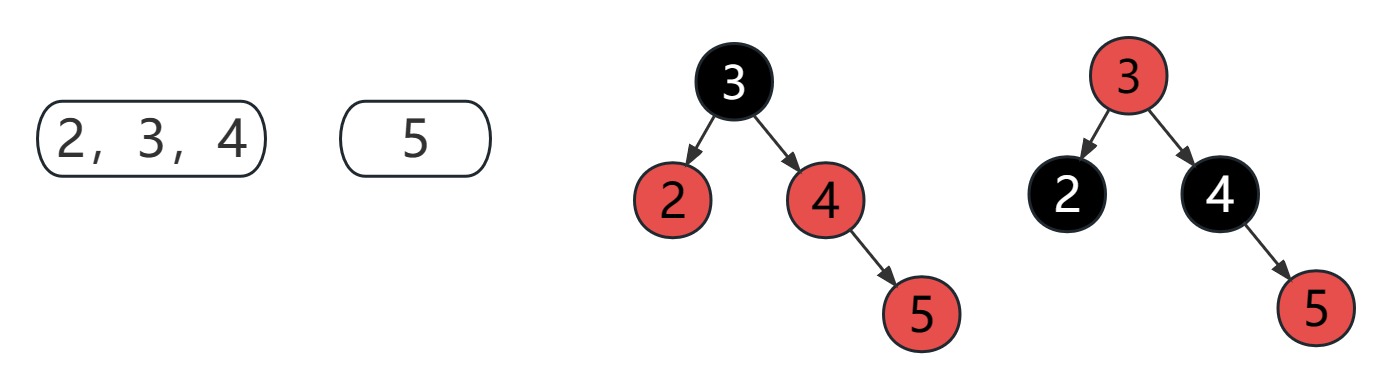
- 黑色节点与它的红色子节点融合在一起,形成 1 个 B 树节点
- 红黑树的黑色节点个数,与 4 阶 B 树的节点总个数相等
- 在所有的 B 树节点中,永远是黑色节点是父节点,红色节点是子节点,黑色节点在中间,红色节点在两边
4 红黑树添加节点的调整
在 2-节点上添加
- 在 2-节点上添加意味着父节点一定是黑,可以直接添加
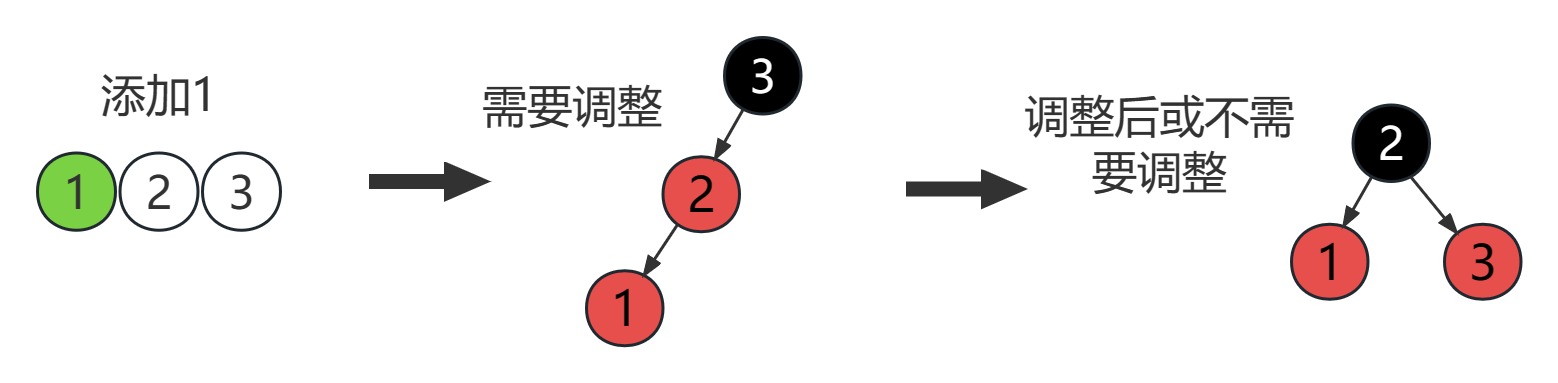
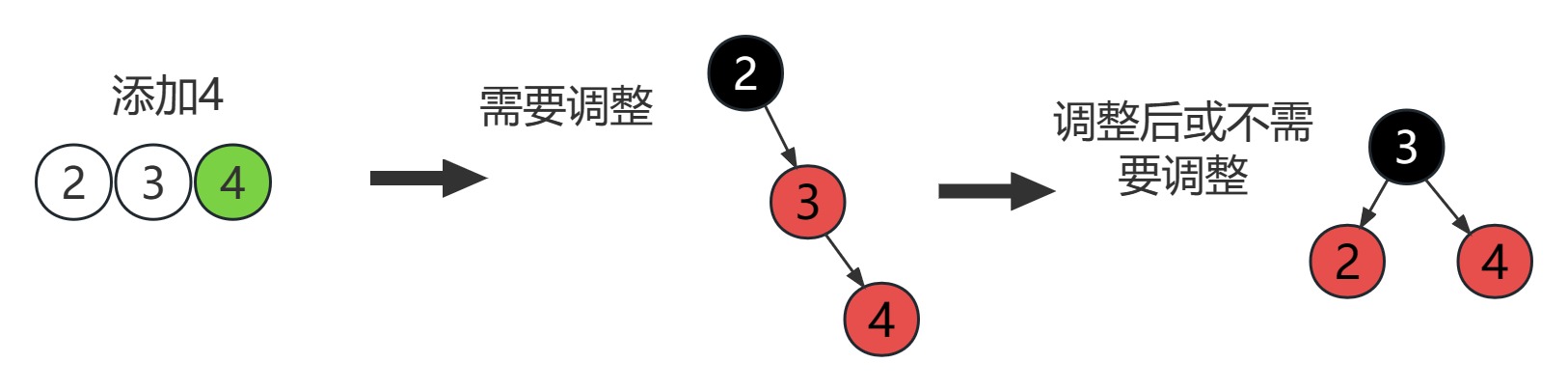
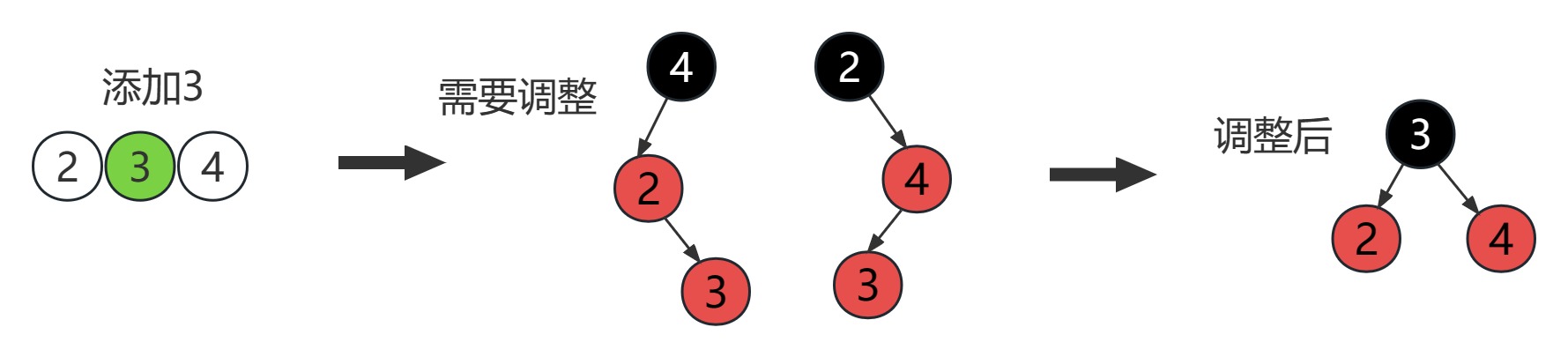
在 3-节点上添加有如下几种情况
LL型需要调整:右旋
RR型需要调整:左旋
LR型需要调整:先父节点左旋形成LL型,然后爷节点右旋
RL型需要调整:先父节点右旋形成RR型,然后爷节点左旋
两种左中右型的不需要调整
在4-节点上添加右如下情况
4-节点新增一个元素,4-节点中间元素升级为父节点,剩下的两个元素和新增元素合并为一个3节点
在红黑树中,新增节点时:新增的节点是红色,新增节点的父节点和叔叔节点也是红色,爷爷节点是黑色。调整为也爷节点变为红色,父节点和叔叔节点变为黑色,如果爷爷节点是root节点,则把也爷节点调整为黑色。如果爷爷节点的父节点也是红色,还应当递归让爷爷节点以上的节点也调整
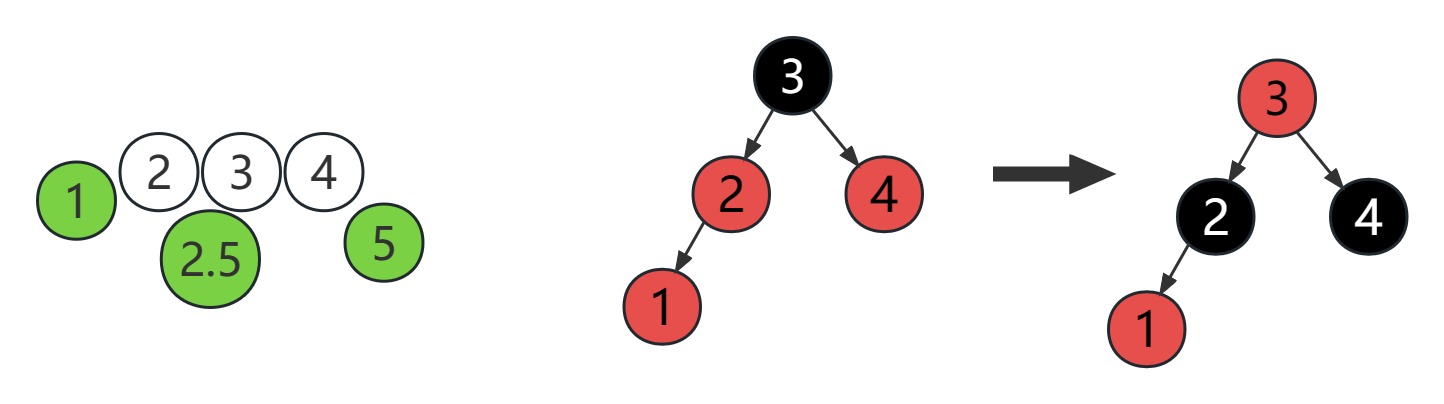
总结为:
- 如果是根节点,变为黑色并返回
- 如果父节点是黑色:
- 2-节点添加:不需要调整直接返回
- 如果父节点是红的,叔节点空或者黑(新添加节点时叔节点一定为空,但往上回溯时叔节点可能为黑)
- 3-节点添加:LL、LR、RL、RR
- 如果父节点、叔节点都是红色
- 4-节点添加:父节点叔节点变黑色,爷节点变红色,如果爷节点的父节点也是红色,则还需要递归调用让爷节点以上的节点继续调整
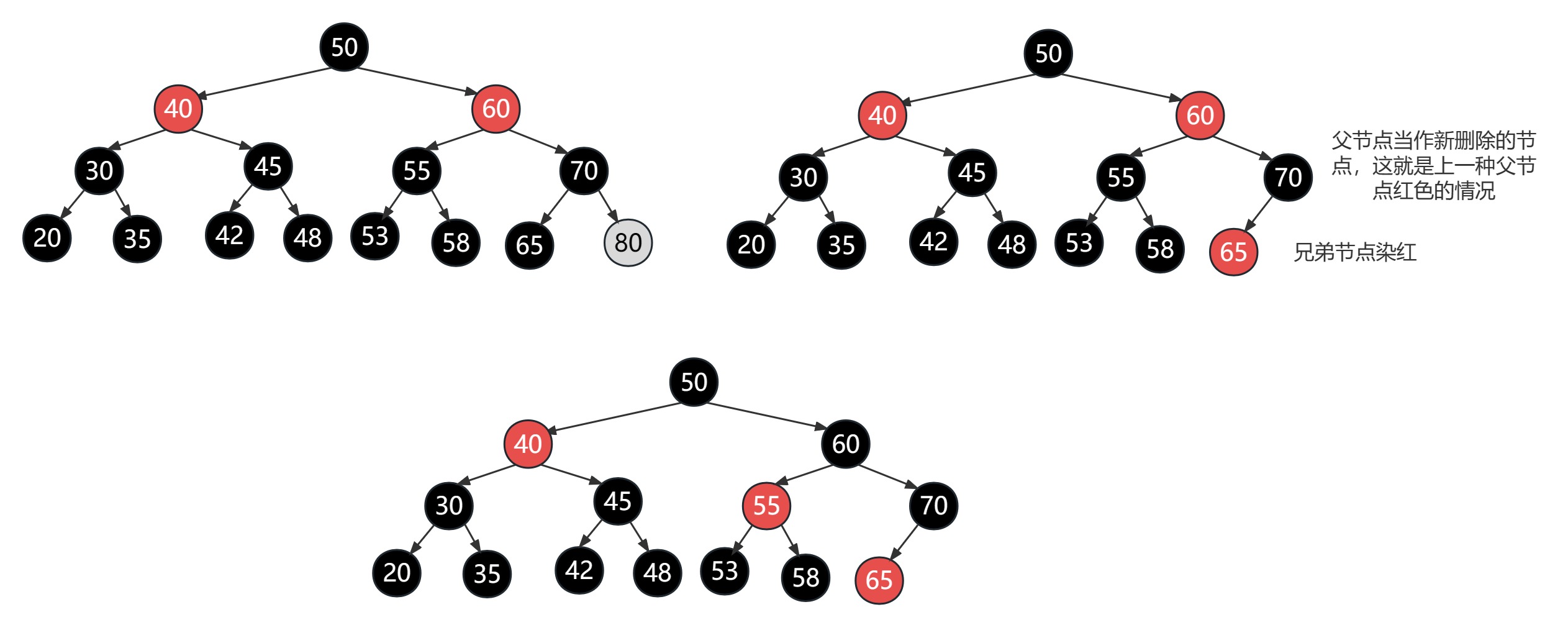
5 红黑树删除节点的调整
5.1 删除节点的情况
- 删除非null的叶子节点
- 如果该叶子节点是红色,可以直接删除
- 如果该叶子节点是黑色,删除后会导致黑高失衡,需要进行平衡调整
- 删除只有一个叶子节点的节点
- 此时该目标删除节点一定是黑色,其叶子节点一定是红色,否则无法满足红黑树性质
- 删除时将红色叶子节点的值复制到目标删除节点中,将删除节点转换为删除红色叶子节点
- 删除有两个子节点的节点
- 使用前驱或后继节点作为删除节点的替代节点,转换为1或2的情况
5.2 删除节点的辅助方法
在删除有两个子节点的节点时,需要寻找前驱和后继节点。获得替代节点的目的是减少调整次数。
- 先找前驱节点,如果前驱节点满足以下任意一种情况,则直接返回前驱节点
- 前驱节点是红色叶子节点
- 前驱节点是有一个红色叶子节点的黑节点
- 否则返回后继节点
5.3 删除节点的步骤
- 没找到删除节点则直接返回
- 如果删除节点是唯一一个节点,则root置为null
- 删除有两个子节点的节点
- 使用前驱或后继节点作为替换的删除节点
- 将delNode指向替换节点,转换为4或5处理
- 删除只有一个子节点的节点时,删除节点只能是黑色,其子节点为红色
- 将红色叶子节点的值复制到目标删除节点
- 将目标删除节点转换为删除红色叶子节点
- 删除叶子节点
- 对要删除的黑色叶子节点进行调整
- 删除红黑两种叶子节点
5.4 删除节点后调整平衡
D-删除节点;P-父节点;B-兄弟节点;NL-左侄子节点;NR-右侄子节点;G-爷爷节点;U-叔叔节点;紫色表示可能是红也可能是黑
删除黑色叶子节点
如果这是树中唯一一个节点,直接删除
兄弟节点是红色
删除右子节点需要右旋
兄弟和右侄颜色互换
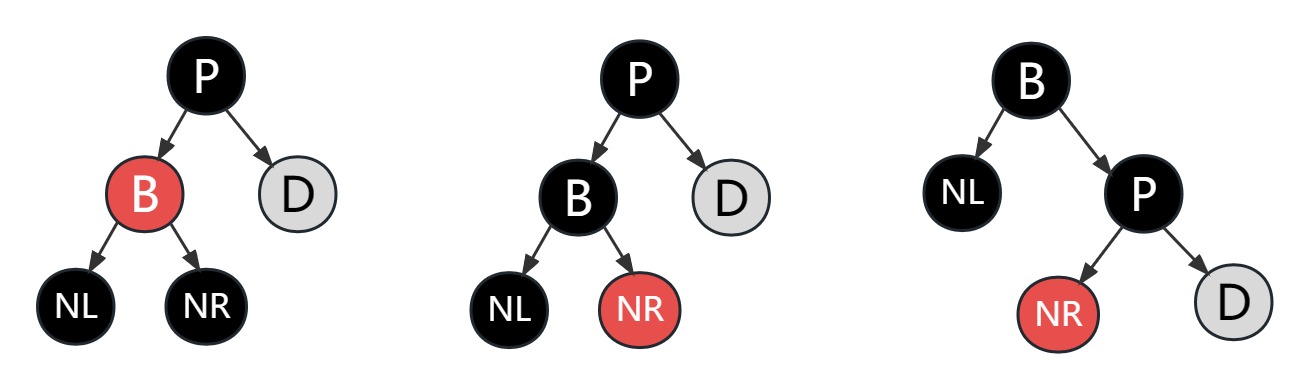
兄弟节点是黑色
兄弟有红色子节点
兄弟有红色左子节点
- LL型:父节点右旋
- 变色:恢复删除前各位置的颜色:爷孙变黑,兄变父色
兄弟有红色右子节点
- LR型,先左旋后右旋
- 变色:恢复删除前各位置的颜色 - 侄变父色,父变黑色
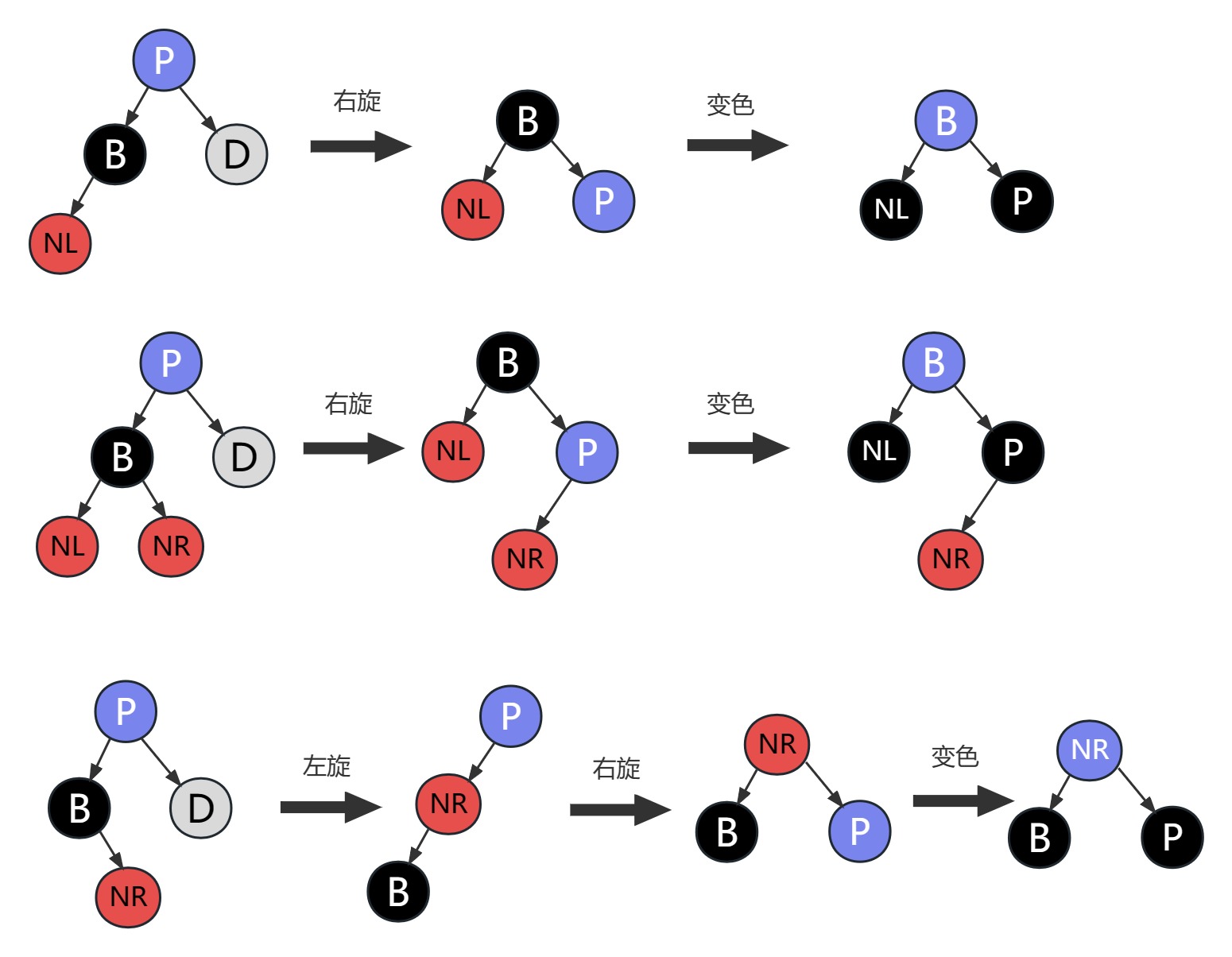
兄弟无红色子节点
父节点是红色:父变黑,兄变红
父节点是黑色:将兄弟染红,然后以父节点为基准(新删除节点)向上递归调整,直至遇到红色父节点并将其染黑或者遇到根节点
5.5 删除节点后的旋转类型
旋转类型看兄弟节点(黑色)及其红色子节点的位置
因为要兼顾到向上回溯调用调整,所以相关类型定义如下
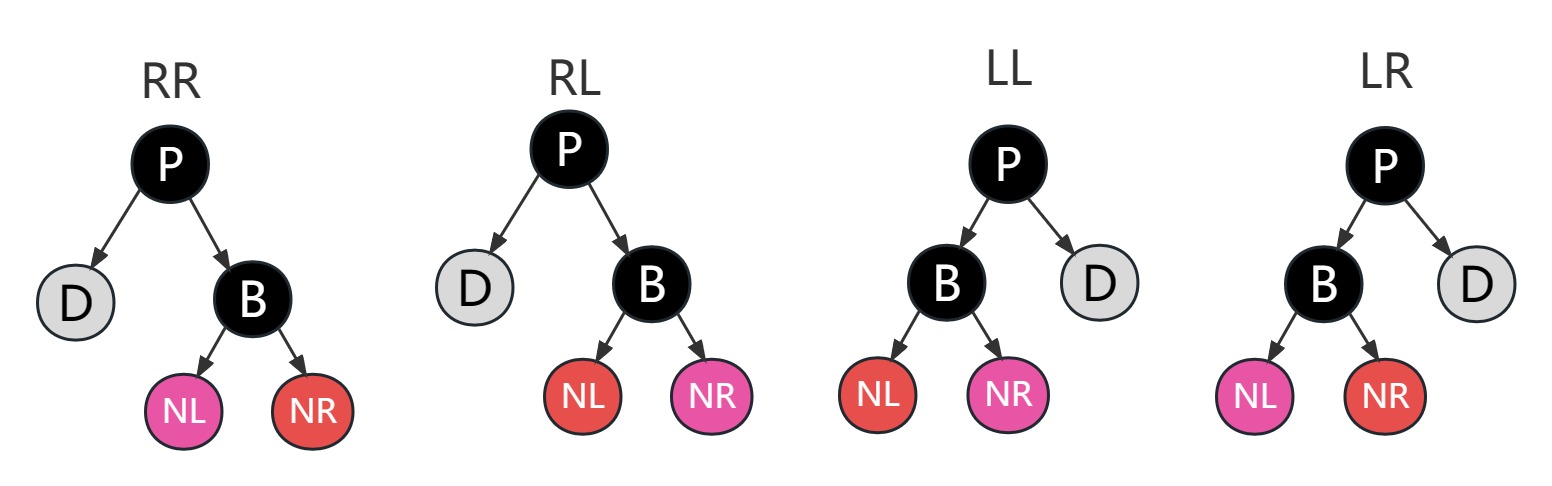
5.6 总结
删除黑色节点调整
- 兄弟黑
- 兄弟有子
- LL、LR、RR、RL
- 兄弟无子
- 父是黑
- 父是红
- 兄弟有子
- 兄弟红
- 删左子
- 删右子
- 兄弟黑
口诀
- 是根节点:直接染黑即可
- 兄弟黑色
- 兄弟有子:黑不够,侄来凑
- 根据LL、LR、RL、RR类型旋转来调整
- 兄弟无子:兄无后,父红头
- 父节点是红色:父变黑,兄变红
- 父节点是黑色:父作为新的删除(调整)节点向上递归调整
- 兄弟有子:黑不够,侄来凑
- 兄弟红色
- 兄弟红,旋黑中;随父侄,黑变红
- 兄弟是左子树:右旋-右侄变红
- 兄弟是右子树:左旋-左侄变红
- 兄弟红,旋黑中;随父侄,黑变红






